At ioxp, Gitlab is our tool of choice to organize our development. We also use their Wiki tool for our employee handbook and this is where we also have a list of all our internal services to maintain an overview about what is deployed, why and where. It looks like this:
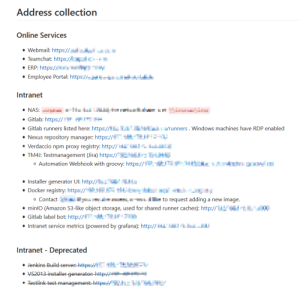
To a) check that every service listed there is reachable and thus b) checking that the list is up-to-date (at least in one direction), we added a special Gitlab CI job which curl’s them all. This is its definition inside our main project’s .gitlab-ci.yml:
The script
Internal IT Check:
only:
variables:
- $CI_CUSTOM_ITCHECK
needs: []
variables:
GIT_STRATEGY: none
WIKI_PAGE: IT-Address-List.md
before_script:
- apk add --update --no-cache git curl
- git --version
- git clone https://gitlab-ci-token:${CI_JOB_TOKEN}@${CI_SERVER_HOST}/wiki/wiki.wiki.git
script:
# Scrape the URLs from the IT wiki page
- cd wiki.wiki
- |
urls="$(cat $WIKI_PAGE | grep -Ev '~~.+~~' | grep -Eo '(http|https)://([-a-zA-Z0-9@:%_+.~#?&/=]+)' | sort -u)"
if [ -z "$urls" ]; then echo "No URLs found in Wiki"; exit 1; fi
- echo "Testing URLs from the Wiki:" && echo "$urls"
# Call each URL and see if it is available. set +e is needed to not exit on subshell errors. set -e is to revert to old behavior.
# Special case: As one of our services does not like curls, we have to set a user agent
- set +e
- failures=""
- for i in $urls ; do result="$(curl -k -sSf -H 'User-Agent:Mozilla' $i 2>&1 | cut -d$'\n' -f 1)"; if [ $? -ne 0 ]; then failures="$failures\n$i - $result"; fi; done
- set -e
- if [ -z "$failures" ] ; then exit 0; fi
# Errors happened
- |
errorText="ERROR: The following services listed in the Wiki are unreachable. Either they are down or the wiki page $WIKI_PAGE is out-dated:"
echo -e "$errorText\033[0;31m$failures\033[0m"
curl -X POST -H "Content-Type: application/json" --data "{ 'pretext': '${CI_JOB_NAME} failed: ${CI_JOB_URL}', 'text': '$errorText$failures', 'color': 'danger' }" ${CI_CUSTOM_SLACK_WEBHOOK_IT} 2>&1
exit 1
Script Breakup
- Gitlab wikis are a git repository under the hood. You can clone them via <projectUrl>.wiki.git (The URL can also be retrieved by clicking on “Clone repository” at the upper right on the wiki main page
- The URLs are extracted by grepping the respective markdown page for http/https links:
grep -Eo '(http|https)://([-a-zA-Z0-9@:%_+.~#?&/=]+)' - To ignore deprecated links (strikethrough in the wiki), we exclude them before with
grep -Ev '~~.+~~'and to filter out duplicates we usesort -uafterwards - Each found URL is then called via curl:
-kdisables the TLS certificate verification if you use self-signed certificates and haven’t installed your own root CA.-H 'User-Agent:Mozilla'was needed because one of our services didn’t like to be curl’ed by a non-browser so we dress up as one.
- With
set +ewe prevent that a subshell error (i.e. the curl) makes the Gitlab job exit with a failure prematurely as we want a list of all errors, not just the first one. - If any error is found, a post containing the list of unavailable services is sent to our IT Slack channel using their webhooks.
Gitlab Preconditions
To run this job in a fixed interval, we set up a scheduled pipeline, running every day at two in the afternoon. The schedule has the variable CI_CUSTOM_ITCHECK defined so the job’s only: selector fires (see in the script above). All other jobs of our pipeline are either defined to not run under schedules or not when the variable is defined (using the except: selector).